亦称“归纳方法的连续统”。卡尔纳普对诸多归纳方法作统一处理,后得到的一个归纳逻辑系统。它借助于状态描述等处理方法,对语言LπN中任意的合式句子h和e定义C-函数,可以归结为对一类特殊的hM和eM,去确定相应的函数值。这类eM报导已经检验过的s个个体中,sM个具有性质M、另外s-sM个不具有性质M,hM则预测尚未经检验的第s+1个个体将具有性质M。C(hM,eM)表示性质M在前s次试验中的出现频度sM/s这一证据,对M在下一次试验中也出现的确证度为量度。显然sM/s这个比是重要的,在确定C(hM,eM)的值时,是必须加以考虑的经验因素。另一个因素由性质谓词M的语形结构决定,称为逻辑因素,记作��,当没有任何证据时,假设hM的确证度将主要由��确定。于是,人们将在经验因素sM/s与逻辑因素��之间取一个加权平均作为C(hM,eM)的值。令sM/s的权重为s,并记㇊的权重为λ,则
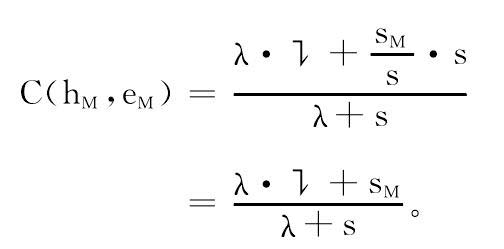
- 内在罪疚
- 内外之合
- 内外体窍图
- 内外控量表
- 内完善原则
- 内容分析
- 内容分析法
- 内容心理学
- 内容效度
- 内导纤维
- 内山喜久雄
- 内心体验
- 内心冲突
- 内心合外物以启觉
- 内心意象
- 内心计数
- 内心计数器
- 内感不适症
- 内投
- 内控、他控、机控量表
- 内控型
- 内控源
- 内控观
- 内插法
- 内攻疗法
- 𭻢
- 𭻣
- 𭻤
- 𭻥
- 𭻦
- 𭻧
- 𭻨
- 𭻩
- 𭻪
- 𭻫
- 𭻬
- 𭻭
- 𭻮
- 𭻯
- 𭻰
- 海岛情书价格是什么意思
- 情感语录啥时发在抖音好是什么意思
- 虐文情感散文阅读推荐书籍是什么意思
- 情感励志诗散文朗诵稿范文是什么意思
- 巴卫情感语录是什么意思
- 散文的情感色彩特点有哪些是什么意思
- 夜景视频情感语录是什么意思
- 情感散文名人素材摘抄简短是什么意思
- 日本言情书籍是什么意思
- 夜晚的情感散文是什么意思
- 无情的情书姜育恒是什么意思
- 情感王子语录短句是什么意思
- 情感励志散文语录素材是什么意思
- 情感散文网站是什么意思
- 表以陈情书是什么意思
- 情侣一定要知道:分手N个高危时刻
- 女子拒绝相亲对象被捅7刀 相亲安全怎么保障
- 表示他已经不爱你的10句话
- 如果男友对你做这3件事,请立即与他分手!
- 如何自我介绍能提高相亲成功率
- 如何识破烂男人的招数
- 如何利用圣诞节挽回男友
- 你怎么看待夫妻AA制?夫妻AA制的必备条件
- 提升恋爱指数5项穿搭法则
- 救命啊,我很爱很爱的人在哪里
- 13个约会细节教你透视男人本质
- 分手指南:女人怎样说分手才能分得漂亮!
- 你的感情有人懂得是一种幸福
- 恋爱出现这8种状况 分手是迟早的事
- 为什么女人提出分手又后悔了?
- 6个月宝宝辅食指南:营养均衡的果泥食谱
- 八月宝宝的健康零食指南
- 8个月宝宝发热时的饮食注意事项
- 三个月宝宝肠炎饮食调理全攻略
- 八个月宝宝断奶后的合理饮食指南
- 三个月宝宝的合理饮食指南
- 一岁宝宝海洋馆游玩攻略:合适的食物选择
- 一岁宝宝辅食食谱:营养均衡的健康选择
- 宝宝吐奶后如何饮食调理?专家支招帮助宝宝快速恢复
- 六月龄宝宝辅食指南:营养均衡的辅食添加方法
- 一周岁宝宝的饮食指南:营养均衡,健康成长
- 宝宝健康成长从第一口鱼开始
- 如何应对三个月宝宝拉稀?专业建议帮您解决问题
- 两岁宝宝辅食指南:营养均衡,助力健康成长
- 7个月宝宝辅食指南:营养均衡的健康饮食