“总体比例假设检验”的意思、起源，总体比例假设检验是由谁提出的-心理学-情感百科-依恋情感网

网站首页情感咨询情感美文情感百科情感生活学习充电旧版美文

标题	总体比例假设检验
类别	心理学
释义	【总体比例假设检验】拼译：test of hypothesis on proportions of population 假设检验的一种。对总体中具有某特征的个体所占比例π的统计检验。如学生中有抑郁症者的比例是否超过20%?经常有下面两种情况：(1)单总体比例的检验。统计假设为H₀：π=π₀；H₁：π≠π₀。(π₀已知)选用的检验统计量是Z=。式中p是随机样本中具有该特征的个体所占比例，n为样本大小。由统计抽样理论可知：在H₀成立时，Z的极限分布为标准正态分布。所以检验应当在大样本条件下进行。对给定的α，查标准正态分布数值表得双侧α分位点－Z_α／2与Z_α／2。若Z的观测值Z₀＞Z_。／2或者Z₀＜－Z_α／2，则否定H₀。对于单侧检验问题，仍使用上述检验统计量，只是临界点为单侧的一个。(2)两总体比例差异的假设检验。设有两个独立的总体，总体比例分别是π₁与π₂。待检验的统计假设是H₀：π₁=π₂=π；H₁：π1≠π₂。从两个总体中各抽一个样本，其样本比例为p₁与p₂。使用的检验统计量为Z=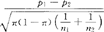。在H₀成立时，渐近地服从N(0，1)。式中的总体比例π并不知道，而用两样本的混合比例(其实是样本比例的加权平均)p^来代替：p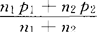^=。对于给定的α，查标准正态分布的双侧α分位点Z_α／2与－Z_α／2。若检验统计量Z的观测值Z₀＞Z_α／2或Z₀＜－Z_α／2时，拒绝H₀。注意，一定要大样本才可进行此检验。
随便看	驾驶员身体素质驾驶员静态视力驾驶员静视野驾驶姿势驾驶实验车驾驶室设计驾驶应激驾驶心理学驾驶技能驾驶效能驾驶期待驾驶模拟实验驾驶注意驾驶环境驾驶疲劳的测定与解除驾驶能力驾驶舱职权梯度驾驶舱领导行为维度驾驶观察驾驶视觉探测驾驶适应性驾驶适应性测试驾驶错觉驾驶错误驾驶音乐 branch entry branch equation Brancher Deficiencies Brancher Deficiency brancher deficiency glycogenosis Brancher deficiency glycogen storage disease brancher enzyme brancher enzyme,branching enzyme brancher glycogen storage disease brancheries branchers branchery branches branches at home and abroad branches,cricothyroid 爱就是抓在手里的一把沙子是什么意思残骸的感情，残骸的情书。残骸的爱，卑微的人。轩是什么意思抬头45°角仰望天空，去触摸头顶上那片蓝天是什么意思痛苦着你的痛苦，欢乐着你的欢乐是什么意思你已在我心裏住太久、、、是什么意思谁虚伪了爱情，谁卑微了承诺是什么意思某人，我曾经喜欢过你，谢谢你的不在乎。。。是什么意思我的爱情就像你手中的蒲公英是什么意思慢慢的才知道太在乎别人了往往会伤害自己是什么意思喂、谢谢你的陪伴和关爱.是什么意思 90后谈恋爱，谈的累不累是什么意思是谁把中国人逼成了爱无能？是什么意思有时，爱只是一种情怀是什么意思永远不要做为爱疯狂的女人是什么意思同居时代,女人内心无言的伤痛是什么意思高情商搭讪聊天的句子狼与狐的恋爱攻略百度网盘出轨后挽回男人的心理方法狼与虎的恋爱攻略小说图片平度情感恋爱婚姻挽回律师 2022年冲绳办婚礼男人老说女孩欺骗他的感情约会烤鱼拍照技巧图片高清前男友信息不回怎么挽回室友粤语情话瓯海婚姻家庭律师电话森林小学举行神秘的婚礼婚礼弹吉他重感情带兔子绰号婚姻家庭纠纷经验交流才料怎么约月亮水瓶座男生太阳上升双子月亮水瓶座的区别太阳水瓶座月亮水瓶座上升金牛的人怎么样太阳金牛座月亮水瓶座女的人怎么样太阳巨蟹座月亮是水瓶座的人怎么样太阳水瓶座和月亮水瓶座合适吗月亮水瓶座配太阳水瓶座合适吗金星水瓶座月亮狮子座女生的人怎么样太阳水瓶座月亮双子座女士的人怎么样金星水瓶座月亮狮子座男生的人怎么样月亮水瓶座月亮白羊座女生配对指数太阳上升水瓶座月亮双鱼座的人怎么样月亮水瓶座月亮水瓶配对指数怎么约月亮水瓶座男生太阳上升双子月亮水瓶座的区别

依恋情感网情感百科知识大全收录了49620条情感类百科知识词条，覆盖心理学、哲学、美学等领域，基本涵盖了日常生活中常见问题的详细解释，是情感生活的有利工具。